I've recently been investigating musical tuning systems, and I've came across something I find quite interesting.
People might be familiar with the differences between Equal Temperament and Just Intonation. To be brief, Equal Temperament is the current system we use, where all twelve musical notes in the chromatic scale are separated by an equal ratio. Whereas Just Tone tuning sets note intervals according to whole number ratios. Equal Temperament intervals approximate Just Tone, but don't quite give a perfect fit. Leading to claims that Equal Temperament is slightly "out of tune."
The following webpage gives a much better explanation of this:
https://pages.mtu.edu/~suits/scales.html
In fact, the information in the table below is essentially copied straight from that page.
(click to enlarge)
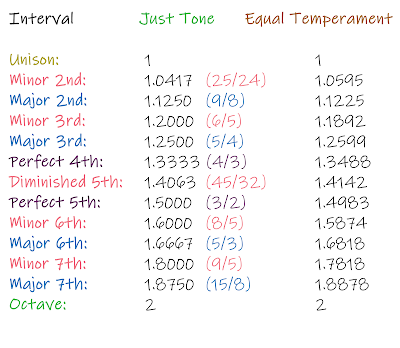
The numbers in the table show the ratio for each interval in each tuning. For example, if we were playing in the key of C, and the first note C was 260 hertz, then the frequency of the C an octave above would be 260 x 2, equalling 520 hertz. Likewise for the Perfect 5th, which in this case would be the note G, the frequency would be 260 x 1.5 (or 3/2), giving us 390 hertz.
However, as you can see from the table. In Equal Temperament tuning the ratio isn't quite 3/2. Instead of a nice round 1.5 we have 1.4983.. So if you want that perfect ratio we aren't quite there. The difference isn't big - using these numbers we would get 389.6 hertz, as opposed to 390 hertz. So for the Perfect 5th it's unlikely you would hear the difference. If you look at the other intervals though you can see that some of the differences are slightly larger. Meaning the discrepancies are somewhat more apparent.
Personally, I'm not overly fussy about tuning perfectly. I'm far too scruffy to be that precise. However, even with my careless playing style I still can't help but be allured by the prospect of more harmonious intervals. So it's fun experimenting with these ideas, and seeing if you can hear (or feel) a noticeable difference.
7/4
Had it just been that I would've experimented with these things in my own music and just left it there. What has really caught my curiosity (and why I'm posting about it here) is something else though.
When I was looking at these tables of ratios I couldn't help but wonder why the ratio 7/4 wasn't used. It's quite a simple, whole number ratio. In fact, it appears quite early on when we work our way up through these fractions.
First we have the unison - that is, a ratio of 1:1. Two notes with the same frequency.
Then we have the octave, 2/1. Where that 1 (the frequency of the original root note) is doubled to take us an octave higher (or halved to take us an octave lower). Doubling again (4/1) would take us two octaves higher, and so on.
Next we move on to divisions by 2. Here, within the octave scale, we only have one, which is 3/2, giving us the previously mentioned Perfect 5th. (2/2 is the same as 1 of course, and 4/2 would be 2, so 3/2 is all we have.)
Then we have to move to 3. Where we have two more important major intervals - the Perfect 4th (4/3), and the Major 6th (5/3). (Again, 3/3 would be 1, and 6/3 would take us back up to 2, the completed octave).
Then comes the divisions by 4. Here we get two more intervals. The Major 3rd (5/4), which is another common and very important interval, that we find in our standard table. Plus another, that we don't - the 7/4, which is the one that so fascinates me. (The eagle-eyed may notice that we've missed out a ratio here, that of 6/4, however 6/4 is the same as 3/2, so it is in fact our old friend the Perfect 5th again, who we've already listed).
The Minors
Incidentally, the next step after this would be to divide by 5. Here we would have 6/5, 7/5, 8/5 and 9/5. These give us the minor intervals. You'll see them all in the table above. That is, except 7/5. Although if you look at the Diminished 5th, which in this table is given by the ratio 45/32, you can see the decimal figure is 1.4063, which is very close to the much neater 1.4 that 7 shared by 5 actually gives us.
(I'm ignoring the Minor 2nd here, which I'll return to later.)
In theory you could move on to divisions of 6 and divisions of 7 and so on. (You can see from the table that the Major 2nd and Major 7th are given by divisions of 8. The 2nd 9/8, the 7th 15/8.)
The Harmonic 7th
Looking at these ratios you can see that 7/4 appears fairly early when we work through these divisions. Only behind the Perfect 5th, Perfect 4th, Major 6th and Major 3rd in the pecking order, and though the 7 itself might make it look slightly odd, it's literally just 1 and 3/4s (4/4 plus 3/4 equalling 7/4), giving us 1.75 as decimal.
Anyway, I looked up the 7/4 online and found it's named "The Harmonic 7th," not because of the 7 itself, but because if played within the octave sequence it would appear where the 7th note would be. Falling somewhere between the Major 6th and the Minor 7th.
Partly thanks to Equal Temperament it is now something of a "lost" interval (as none of the twelve equal temperament intervals approximate it - meaning on a guitar it doesn't have a fret spacing, and on a piano it doesn't have a piano key *sad face*). According to Wikipedia chords containing the interval are now "lost chords".
Its last refuge is apparently barbershop music, and it's said to be a distinctive aspect of that genre.
(I'm largely ignorant of barbershop music, saving that episode of The Simpsons, where Homer and Apu form a barbershop quartet. I will now look into it though. In fact, I did briefly listen to a YouTube talk about it last night as I was drifting off to sleep. It stated that it possibly had origins in monastic vocal music, so the history appears quite deep. I wonder if the harmonic 7th has persisted in this form of music as the singers are unconstrained by instrumentation, which over recent centuries has been restricted to specific tunings.
This is the key question for me: has the 7/4 interval fell from favour because it doesn't sound very pleasing and harmonious - i.e. because people just don't like it; or, has it fell from favour thanks to common and convenient tuning standards?)
A Beautiful Symmetry
What I found when I added it to the chromatic scale was that it brought a beautiful symmetry - at least from a mathematical point of view. (I've also started trying to include it in actual music, though it's difficult given that instruments and music software aren't set up for the option. We'll see what fruit this bears as I plough on.)
In this table I've added the Harmonic 7th, and I've also removed the Minor 2nd. If you consult the earlier table you'll see that the ratio for that interval (25/24) was particularly cumbersome. It's actually quite a dissonant interval too. Famously it's the interval used for the theme to the movie Jaws - the duh-nuh ..duh-nuh ..duh-nuh, duh-nuh, duh-nuh, duh-nuh, duuuhh-nuh. That discord is obviously great for when a pleasant day at the beach is suddenly disrupted by something lurking in the water. It's not nice for songs in general though. (This is one of the great things about music - there is no right or wrong really. It depends what you want).
I've cheekily gotten rid of the interval though. If we look at the table we now have a nice symmetry centred around the Perfect 5th thanks to it. With each pair moving out in ripples, adding up to create a whole. The 1.75 of the Harmonic 7th mirroring the 1.25 of the Major 3rd, and so forth.
It looks nice, but will it sound nice? As per the question earlier. Ultimately the proof is in the playing (and the listening), so I look forward to messing around with this scale.
Hopefully I'll have some more posts on this topic in the future.



Comments
Post a Comment